آلبرت انیشتین فیزیکدان برجسته‌ی آلمانی در سال ۱۸۷۹ میلادی متولد شد. او در طول حیات خود در دانشگاه‌ها و موسسات تحقیقاتی در کشورهای مختلف به فعالیت پرداخت. فعالیت‌های او تأثیر بسزایی در پیشرفت شاخه‌های مختلف علم فیزیک و هم‌چنین فلسفه داشت. تلاش‌های انیشتین، جایزه‌ی نوبل فیزیک را در سال ۱۹۲۱ میلادی در اثر کشف اثر فوتوالکتریک برای او به ارمغان آورد. انیشتین اگرچه جزو پا‌یه‌گذاران علم فیزیک مدرن در دهه‌های ابتدایی قرن بیستم بود، شهرت عمده‌ی او به دلیل ارائه‌ی دو نظریه‌ی نسبیت خاص (۱۹۰۵ میلادی) و نسبیت عام (۱۹۱۵ میلادی) در نجوم نظری است. به تازگی یک‌صدمین سالگرد ارائه‌ی نظریه‌ی نسبیت‌عام توسط انیشتین را پشت‌سر گذاشته‌ایم. به همین مناسبت در این مقاله بر آن شدیم تا به زبانی ساده به معرفی و توضیح دو نظریه‌ی نسبیت خاص و عام بپردازیم.
نظریه‌ی نسبیت خاص
نظریه‌ی نسبیت خاص که در سال ۱۹۰۵ توسط انیشتین ارائه شد، به بررسی قوانین فیزیکی از دید مشاهده‌گرهایی که با سرعت ثابت نسبت به یکدیگر در حال حرکت هستند، می‌پردازد. طبق این نظریه ۱) قوانین فیزیک از دید تمامی ناظرهایی که با سرعت ثابتی نسبت به یکدیگر در حال حرکت هستند، یکسان است، ۲) سرعت نور در خلأ، مستقل از سرعت چشمه‌ی تابش‌کننده‌ی آن، برای تمامی ناظرها یکسان است. بخش اول این نظریه به نسبی‌بودن حرکت اشاره دارد؛ برای مثال در همین لحظه که شما در یک موقعیت ثابت نسبت به کامپیوتر خود قرار دارید، موقعیت شما نسبت به کهکشان‌های دوردست با سرعت بالایی در حال تغییر است. طبق نظریه‌ی نسبیت خاص، آنچه که ما در کره‌ی زمین به عنوان قوانین علم فیزیک می‌پذیریم، مستقل از موقعیت ما می‌باشد و در سایر کهکشان‌ها نیز به همین شکل برقرار است. به این ترتیب، ما در گوشه‌ای از عالم در چارچوب خاص و برتری قرار نداریم. طبق بخش دوم این نظریه، نسبی‌یودن حرکت شامل سرعت نور نمی‌باشد و سرعت نور در خلأ مستقل از سرعت جسم فرستنده‌ی آن از دید تمامی ناظرها برابر با ۳۰۰،۰۰۰ کیلومتر بر ثانیه است.
نظریه‌ی نسبیت خاص نتایج بسیار جالبی با خود به همراه داشت که از جمله‌ی آنها می‌توان به نسبی‌بودن زمان، انقباض طول و هم‌ارزی ماده و انرژی اشاره کرد که در اینجا به‌طور مختصر به توضیح آنها می‌پردازیم.
نسبی بودن زمان
شکل ۱: کندتر گذشتن زمان برای ناظری که با سرعت‌های نسبیتی در حال حرکت است نسبت به ناظر زمینی.
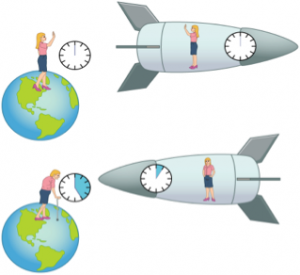
تا پیش از نظریه‌ی نسبیت انیشتین، زمان از دید فیزیکدانان یک مفهوم مطلق و مستقل از حرکت مشاهده‌گر بود، اما یکی از نتایج نظریه‌ی نسبیت ارائه یک تعریف نسبی از زمان و هم‌زمانی است. طبق این نظریه، هم‌زمان بودن دو رویداد از دید یک ناظر در سطح کره‌ی زمین به معنی هم‌زمان‌بودن آنها از دید یک فضانورد که در سفینه‌ی خود در حال مشاهدهی این دو رویداد است، نمی‌باشد. هم‌چنین بر اساس نسبیت خاص، نرخ گذر زمان برای جسمی که مشاهده میشود بستگی به سرعت جسم و سرعت مشاهده‌گر دارد. برای مثال، یک ساعت زمینی معادل با ۵۲ دقیقه برای ناظری است که با سرعتی برابر با نصف سرعت نور از ما در حال دور شدن است (شکل ۱).
انقباض طول
طول یک جسم وابسته به سرعت ناظر در حال اندازه‌گیری است و هر چه سرعت ناظرها بیشتر باشد طول کمتری برای جسم اندازه خواهند گرفت (شکل ۲). البته اختلاف در این اندازه‌گیری‌ها برای ناظرهایی که با سرعت‌های بسیار کمتر از سرعت نور حرکت میکنند ناچیز است. برای مثال، طول یک میله‌ی یک متری برای ناظری که با سرعتی برابر با نصف سرعت نور در حال دورشدن از زمین است، برابربا ۸۶/۶ سانتی‌متر خواهد بود.
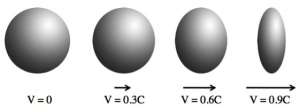
شکل ۲: برای ناظرهایی که با سرعت‌های نسبیتی در راستای قطر کره در حال حرکت هستند، اندازه‌ی قطر متفاوت از اندازه‌ی ناظر ساکن نسبت به کره خواهد بود. هرچه سرعت ناظرها بیشتر باشد شکل کره از دید آنها بیضوی‌تر میشود.
هم‌ارزی ماده و انرژی
در مکانیک نیوتونی در سرعت‌های پایین، جرم یک جسم مستقل از سرعت آن، مقداری ثابت است، اما در سرعت‌های نسبیتی جرم نیز همچون طول و زمان از دید مشاهده‌گرهای مختلف متفاوت خواهد بود. در حالی‌که از دید ناظر ساکن نسبت به یک جسم، جرم جسم برابر با جرم اندازه‌گیری‌شده در مکانیک نیوتونی است، از دید ناظر در حال حرکت جرم این جسم کمتر خواهد بود. ناظر در حال حرکت – که خود را ثابت و جسم را در حال حرکت می‌بیند – جرم ازدست‌رفته توسط جسم را تبدیل‌یافته به انرژی جنبشی می‌داند. این بدین معنی است که در محدوده‌ی سرعت‌های نزدیک به سرعت نور، جرم و انرژی قابل تبدیل به یکدیگر هستند و اصل پایستگی ماده-انرژی در قلمرو نسبیتی برقرار است. بر طبق این اصل، میزان انرژی هر جسم برابر است با E=mc۲ که در این رابطه، m جرم جسم در حال سکون و c سرعت نور در خلأ است. یک جسم ۱ کیلوگرمی که با سرعتی برابر با نصف سرعت نور در حال حرکت نسبت به زمین است، از دید ناظر زمینی جرمی تقریبا برابر با ۸۶۶ گرم خواهد داشت. افزایش سرعت جسم از دید ناظر زمینی، همراه با کاهش میزان جرم اندازه‌گیری‌شده‌ی آن خواهد بود. در نهایت برای ذراتی که قابلیت حرکت با سرعت نور را دارند (برای مثال فوتون‌ها)، میزان جرم اندازه‌گیری‌شده در یک چارچوب ثابت همچون یک آزمایشگاه به صفر کاهش خواهد یافت.
مفهوم فضا-زمان
شکل ۳: تصویری شماتیک از یک فضا-زمان ۴بعدی.
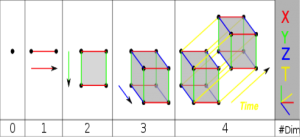
بر اساس فرضیات هندسه‌ی اقلیدسی، جهان سه بعد مکانی و یک بعد زمانی مستقل از هم دارد. اما با خارج شدن زمان از شکل یک کمیت مطلق در نسبیت، دو مفهوم فضا و زمان با یکدیگر ادغام می‌شوند و یک محیط پیوسته‌ی چهاربعدی را ایجاد میکنند (شکل ۳). به این ترتیب در نسبیت مختصات هر جسم با ۴ مؤلفه‌ی بردار فضا-زمان (t,x,y,z) توصیف میشود.
نظریه‌ی نسبیت عام
درحالی که نظریه‌ی نسبیت خاص به بررسی قوانین فیزیک در چارچوب‌هایی که با سرعت ثابت (در محدوده‌ی سرعت‌های نزدیک به سرعت نور) نسبت به یکدیگر در حال حرکت هستند، می‌پردازد، این پرسش پیش می‌آید که در صورت شتابداربودن حرکت این چارچوب‌ها، قوانین فیزیک به چه شکل خواهند بود. انیشتین در سال ۱۹۱۵ با ارائه‌ی نظریه‌ی نسبیت عام به این پرسش پاسخ داد.
شکل ۴. هم‌ارزبودن حرکت در سیستم‌های شتابدار و حرکت در میدان گرانشی.
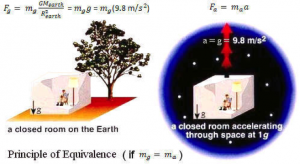
انیشتین با درنظرگرفتن این نکته که بررسی یک دستگاه در حال حرکت با شتاب ثابت، معادل با سقوط آزاد دستگاه در یک میدان گرانشی با همان شتاب است، گرانش را وارد مسئله کرد. به شخصی که در یک آسانسور در حال حرکت با شتاب g قرار دارد، همان میزان نیرو وارد میشود که به این شخص در سطح کره‌ی زمین وارد خواهد شد. این شخص چه در داخل آسانسور، چه در سطح کره‌ی زمین نیرویی برابر با mg را حس خواهد کرد. انیشتین با هم ارز دانستن حرکت شتابدار و حرکت در میدان گرانشی، به جای بررسی حرکت در یک چارچوب با شتاب a به بررسی حرکت همان جسم در میدان گرانشی با شتاب a پرداخت (شکل ۴).
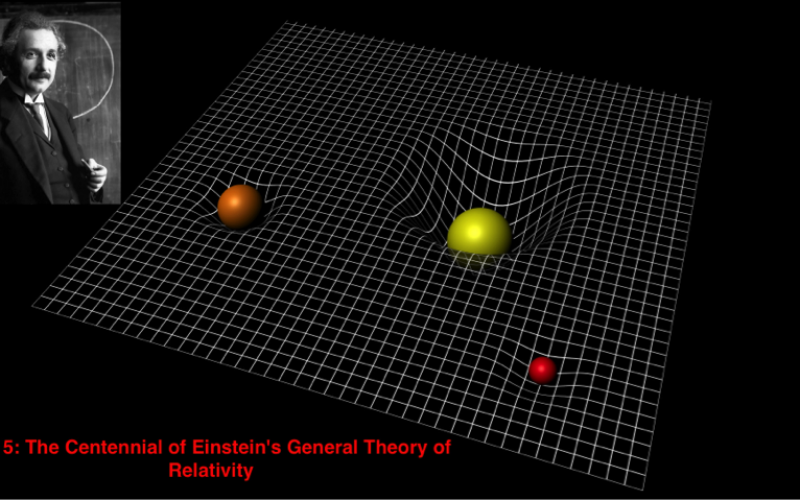
اما میدان گرانشی نیز در نسبیت مفهومی متفاوت از فیزیک کلاسیک دارد. گرانش درنسبیت به عنوان خاصیتی از فضا-زمان در نظر گرفته میشود، به نحوی که هر جسم جرم‌دار، فضا-زمان اطراف خود را دچار خمیدگی می‌کند. در فواصل دورتر که اثر گرانش جسم ناچیز میشود، این انحنا از بین رفته و فضا-زمان تخت خواهد بود. هر چه میزان جرم یک جسم بیشتر باشد خمیدگی ایجادشده در فضا-زمان اطراف آن نیز بیشتر خواهد بود (شکل ۵). به بیان دیگر میزان ماده در یک فضا تعیین‌کننده‌ی خمیدگی و هندسه‌ی فضا-زمان است.
شکل ۵: تصویر شماتیک از یک فضا-زمان ۴بعدی که اجسام مختلف آن را دچار انحنا میکنند. هرچه جرم جسم بیشتر میشود فضا -زمان اطراف آن خمیدگی بیشتری خواهد داشت.
انیشتین این نکته را در فرمول‌بندی ریاضی تحت عنوان معادله‌ی نسبیت عام ارائه کرد:
سمت چپ این معادله‌ی پیچیده که به صورت یک تانسور مرتبه دوم است، توصیف‌کننده‌ی خمیدگی و هندسه‌ی فضا-زمان است و سمت راست آن میزان ماده را فرمول‌بندی می‌کند (در این مقاله، ما به جزئیات این معادله‌ی تانسوری نمی‌پردازیم). اما حل این معادله‌ی غیرخطی بسیار دشوار است، از این‌رو طی ۱۰۰ سال گذشته منجمان و کیهان‌شناسان با روش‌های تقریبی و شبیه‌سازی به حل این معادله پرداخته‌اند.
از جمله‌ی معروف‌ترین تقریب‌ها برای حل این معادله، تقریب شوارتزشیلد(۱) است که کارل شوارتزشیلد در سال ۱۹۱۶ ارائه کرد. این حل تقریبی که میدان گرانشی را بیرون جسمی با تقارن کروی توصیف می‌کند، با فرض بار الکتریکی صفر و گشتاور زاویه‌ای صفر در فضایی بدون هیچ ماده‌ی دیگری به حل معادله‌ی فوق می‌پردازد. این پاسخ تقریب خوبی برای توصیف میدان گرانشی ستاره‌هایی که به کندی می‌چرخند همانند خورشید و سیاره‌هایی همچون زمین می‌باشد اما برای یک سیاهچاله با جرم بسیار سنگین، اندازه‌حرکت زاویه‌ای و بار الکتریکی این روش تقریبی پاسخگو نیست. راه‌حل‌های تقریبی دیگر نیز با درنظرگرفتن گشتاور زاویه‌ای و بار الکتریکی برای حل معادله انیشتین ارائه شده‌اند که از جمله‌ی آنها می‌توان راه‌حل‌های کر(۲) و رایسنر-نوردستروم(۳) را نام برد. هر یک از این راه‌حل‌های تقریبی نیز دارای پیچیدگی‌های ریاضی زیادی هستند که پرداختن به جزئیات آنها خارج از مجال این مقاله است، به همین جهت در ادامه تنها به معرفی برخی از پیش‌بینی‌ها و کاربردهای نظریه‌ی نسبیت عام می‌پردازیم.
شکل ۶. حرکت تقدیمی نقطه‌ی حضیض یک سیاره در حرکت خود به دور خورشید.
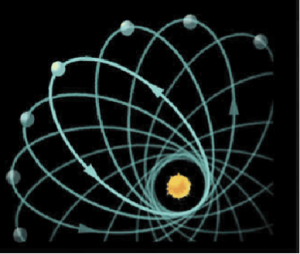
انیشتین و سایر منجمان برای تأیید نظریه‌ی نسبیت انیشتین از چندین آزمایش استفاده کردند. یکی از این آزمایش‌ها بررسی مدار حرکت عطارد حول خورشید بود که مشاهدات رصدی آن با پیش‌بینی مکانیک کلاسیک نیوتونی متفاوت بود. مدار حرکت سیارات به دور خورشید بیضوی است. کمترین فاصله‌ی سیاره تا خورشید در این مدار نقطه‌ی حضیض نامیده میشود. حضور سیارات دیگر در منظومه‌ی شمسی، مدار هر سیاره را کمی دچار اغتشاش می‌کند و سبب حرکت تقدیمی نقطه‌ی حضیض میشود (شکل ۶). اما حرکت تقدیمی نقطه‌ی حضیض عطارد با آنچه که مکانیک نیوتونی پیش‌بینی می‌کرد تفاوت داشت. انیشتین محاسبات کلاسیکی را با درنظرگرفتن اثر خمیدگی فضا-زمان توسط گرانش خورشید تصحیح کرد و نتیجه‌ای که به دست آورد با اندازه‌گیری‌های رصدی کاملا مطابق بود.
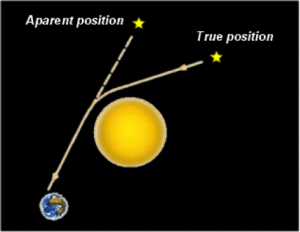
یکی دیگر از نتایج نسبیت عام انیشتین پیش‌بینی انحنای پرتوهای نور در عبور از کنار یک جسم سنگین بود. طبق نسبیت عام، نور هنگام عبور از یک میدان گرانشی در خط مستقیم سیر نمی‌کند، بلکه مسیر آن توسط جسم سنگین خم میشود (شکل ۷). این نکته را می‌توان با مشاهدهی نور ستارگانی که نزدیک به خورشید دیده می‌شوند، هنگام یک خورشیدگرفتگی آزمود. اگرچه قبل از انیشتین، افرادی همچون هنری کاوندیش با مکانیک نیوتونی پی به این نکته برده بودند، اما انیشتین با نسبیت عام میزان دقیق این انحراف را اندازه‌گیری کرد.
شکل ۷. انحنای پرتوهای نور در عبور از میدان گرانشی یک جسم سنگین.
این نکته هم‌چنین سبب پیش‌بینی همگرایی گرانشی(۴) شد که در آن نور یک چشمه‌ی درخشان بسیار دور، مانند یک ابرنواختر، در مسیرش به سمت ما، از کنار جسم پر جرم دیگری مانند یک خوشه‌ی کهکشانی می‌گذرد و مسیرش خمیده میشود. میدان گرانشی جسم میانی، برای مثال خوشه‌ی کهکشانی، همچون یک عدسی رفتار می‌کند و سبب بهتر دیده‌شدن نور جسم دوردست میشود. همگرایی گرانشی امروزه یکی از روش‌های بسیار شناخته شده در مطالعات نجومی است.
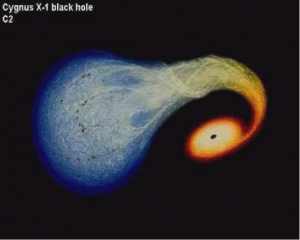
یکی دیگر از پیش‌بینی‌های نظریه‌ی نسبیت عام وجود سیاهچاله‌ها بود. اگرچه پیش از انیشتین نیز در قرن ۱۸ میلادی جان میشل و لاپلاس وجود چنین اجسامی را پیش‌بینی کرده بودند. نسبیت عام در ادامه اثر گرانش بر روی نور، پیش‌بینی می‌کرد که برای یک جسم بسیار سنگین و فشرده، نیروی گرانشی می‌تواند به قدری قوی باشد که حتی نور ناشی از جسم نتواند از این میدان فرار کند. اما تا سال‌ها بعد وجود سیاهچاله صرفا یک پیش‌بینی ناشی از محاسبات ریاضی بر روی کاغذ بود و وجود ناحیه‌ای در فضا که چیزی، حتی نور، نمی‌توانست از آن بگریزد به خوبی درک نمی‌شد. نهایتا در سال ۱۹۷۰میلادی با پیشرفت نجوم رصدی، با کشف ۲ ستاره در قلب صورت فلکی ماکیان(۵) وجود سیاهچاله‌ها برای اولین بار تایید شد. در این سیستم دوتایی پرجرم که تابشگر قوی پرتو ایکس هستند، یکی از دو ستاره تبدیل به یک سیاهچاله شده و در حال بلعیدن ستاره‌ی دوم است. به این ترتیب جریان ماده از سمت ستاره‌ی دوم به سمت این سیاهچاله امکان رصد این سیاهچاله را فراهم کرده است (شکل ۸). تلسکوپ‌های امروزی حتی وجود سیاهچاله‌های بسیار سبک‌تر را نیز تایید میکنند.
شکل ۸. سیاهچاله‌ی صورت فلکی ماکیان که در حال بلعیدن ستاره‌ی مجاور خود است.
پیش‌بینی‌ها و کاربردهای نسبیت عام انیشتین تنها محدود به موارد نامبرده‌ی فوق نیست و شامل موارد دیگری نیز همچون وجود امواج گرانشی، انتقال‌به‌سرخ گرانشی، و موارد دیگر نیز می‌باشد که هر یک را می‌توان در مقاله‌ای جداگانه بررسی کرد.
بدون شک دو نظریه‌ی نسبیت خاص و عام انیشتین و تلاش‌های او در فیزیک مدرن، تأثیر بسزایی در پیشرفت علم فیزیک داشت. انیشتین در سال ۱۹۵۵ میلادی در شهر پرینستون در ایالت نیوجرسی آمریکا درگذشت.
(۱) Schwarzschild
(۲) Kerr
(۳) Reissner–Nordström
(۴) Gravitational Lensing
(۵) Cygnus
نویسنده: مژگان آزادی
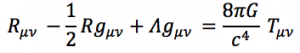
سلام
دم شما گرم… خسته نباشید.
خیلی عالی بود ولی کاش اسم اینشتین را درست می‌نوشتید.
سلام
بسیار عالی. ممنونم.
بسیار عالی. فقط بنظرم یک ایراد کوچیک داشت. در قسمت نظریه خاص، در بخش مربوط به هم ارزی جرم و انرژی یک اشتباه به طور مکرر انجام میشود و آن این است که جرم را متغیر میگیرند ولی باید توجه کرد که جرم از خواص ذاتی است همانند بار اسپین و…. این که جملات مربوط به گاما و تصحیحات نسبیتی را در جرم وارد کنیم و جرم را متغیر بگیریم اشتباه مرسومی است که در بسیاری جاها انجام میشه، در حقیقت در فرمول بندی نسبیتی ما با تعریف سرعت های تعمیم یافته بصورت چاربردار فرض میکنیم جرم جسم همچنان ثابت است. این رهیافت علمی تر است ولی همچنان رهیافت ارایه شده در این مقاله نیز مورد استفاده قرار میگیرد که کمی ملموس تر و جالب تر است ولی رهیافت درست تا جاییکه من میدونم این هستش که جرم ثابت است
عالی بود
سلام، خیلی عالی و قابل فهم توضیح داده شده، مرسی.
ممنون از شما دوستان که مقالات اسطرلاب رو دنبال می‌کنید. :)
سلام مقاله شما خوب هستش
من دنبال معادله حرکت خورشید از ناظر زمینی هستم ممنون میشم راهنمایی کنید
سلام ممنون از مطلب مفیدتون. سوالی داشتم در مورد بحث دوقلوها. وقتی سفینه در حال برگشت به زمین است، به علت اینکه مجبور به تغییر سرعت است، حرکت آن شتابدار خواهد بود و لذا دیگر دستگاه مرجع لخت نیست، آیا در این صورت نتیجه ای که ما می گیریم مبنی بر اینکه شخص داخل سفینه جوان تر خواهد ماند صحیح است؟
ممنون
سلام خانم آزادی من میخوام از طریق کارهای محققی در زمینه فیزیک به یک کشور خارجی مهاجرت کنم ولی نمیخوام وارد دانشگاه بشم و فقط مدرک در زمینه مهندسی برق است و علاقه زیادی به فیزیک دارم میشه بدون مدرک ولی با مقاله های فراوان وارد یک کشور خارجی شد اصلا آنها ما را با ایم شرایط قبول میکنند