تورم – Inflation

Inflation |inˈflāSHən|

تاریخ کیهان. تورم کمی پس از مهبانگ رخ داده است.

تورم

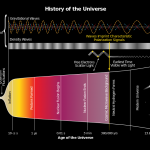
یا تورم کیهانی یک نظریه‌ی کیهان‌شناسی است که بر اساس آن کیهان اولیه در دوران کوتاهی (کسری از ثانیه) پس از مهبانگ انبساط بسیار سریع (نمایی) داشته است. پس از تورم، کیهان به انبساط خود ادامه داده است اما با آهنگی آرام‌تر.

نظریه‌ی تورم در دهه‌ی ۱۹۸۰ میلادی برای توضیح برخی از مشکلات نظریه‌ی مهبانگ استاندارد، که بر طبق آن کیهان به آرامی منبسط می‌شود، ارائه شد. اصلی‌ترین مسائلی که نظریه‌ی تورمی آن‌ها را توضیح می‌دهد شامل موارد زیر می‌شود:

• مساله‌ی تخت‌بودن کیهان (The Flatness Problem)
  بر اساس نظریه‌ی مهبانگ انحنا با زمان رشد پیدا می‌کند. برای آنکه کیهانی به تختی آنچه امروزه می‌بینیم داشته باشیم، لازم است که شرایط بسیار خاصی در گذشته‌ی کیهان وجود داشته باشد؛ احتمال آنکه این شرایط بسیار خاص اتفاقی رخ داده باشند بسیار کم است.
• مساله‌ی افق (The Horizon Problem)
  نواحی دوردست فضا در جهت‌های مخالف یکدیگر در آسمان آنقدر از یکدیگر دور هستند که با در نظر گرفتن انبساط استاندارد مهبانگ هیچ‌گاه نمی‌توانند با هم در تماس علّی باشند. علت این قضیه این است که زمانِ نوری بین آن‌ها (زمانی که طول می‌کشد نور بین آن‌ها سفر کند) از سن کیهان بیشتر است. این در حالی است که یکدست بودن دمای تابش زمینه‌ی کیهان نشان می‌دهد که این مناطق باید در گذشته با یکدیگر در تماس بوده باشند.
• مساله‌ی تک‌قطبی (The Monopole Problem)
  کیهان‌شناسی مهبانگ پیش‌بینی می‌کند که تعداد بسیار زیادی «تک‌قطبی مغناطیسی» باید در کیهان اولیه به وجود آمده باشد. اما تک‌قطبی‌های مغناطیسی تا به حال مشاهده نشده‌اند؛ بنابراین حتی اگر وجود داشته باشند خیلی نادرتر از آچه مهبانگ استاندارد پیش‌بینی می‌کند باید باشند.

تورم اندازه‌ی خطی کیهان را حدود ۱۰ به توان ۲۶ بار در کسری از ثانیه افزایش می‌دهد! امروزه این نظریه متممی بر نظریه‌ی مهبانگ استاندارد به حساب می‌آید، چرا که این مسائل را به خوبی توضیح می‌دهد، اما چگونه؟

• مساله‌ی تخت‌بودن کیهان (The Flatness Problem)
  تصور کنید روی سطح یک توپ (یک دنیای دوبعدی) زندگی می‌کنید. در این شرایط احتمالا برای شما واضح است که روی یک سطح انحنادار هستید (کیهان بسته). حالا اگر این توپ را به اندازه زمین منبسط کنیم، سطحی که روی آن زندگی می‌کنید به نظرتان مسطح می‌آید، گرچه در مقیاس‌های بزرگتر همچنان یک کره است. حالا تصور کنید ابعاد توپ را به اندازه‌ی مقیاس‌های نجومی بزرگ کنیم. در این حالت این فضا برای شما تا جایی که می‌بینید تخت به نظر می‌آید، گرچه در ابتدا یک سطح انحنادار بود. تورم هر انحنای اولیه‌ی کیهان سه بعدی را تا نزدیکی تخت‌بودن متسع می‌کند.
• مساله‌ی افق (The Horizon Problem)
  تورم یک انبساط بسیار سریع نمایی در کیهان اولیه است. بنابراین نواحی دوردست فضا در ابتدا در واقع بسیار از آنچه که با انبساط تدریجی مهبانگ پیش‌بینی می‌شود به هم نزدیک‌تر بوده‌اند. به این ترتیب، این نواحی پیش از تورم تماس علّی داشته‌اند و به همین علت هم‌دما شده‌اند.
• مساله‌ی تک‌قطبی (The Monopole Problem)
  تورم اجازه می‌دهد که تک‌قطبی‌های مغناطیسی تا زمانی که پیش از دوران تورم به وجود آمده باشند، وجود داشته باشند. در دوران تورم چگالی تک‌قطبی‌های مغناطیسی ناگهان افت می‌کند و به این ترتیب فراوانی آن‌ها بسیار بسیار کم می‌شود طوری که قابل آشکارسازی نیستند.

نظریه‌ی تورم همچنین نحوه‌ی شکل‌گیری ساختارهای بزرگ‌مقیاس کیهان (ستاره‌ها، کهکشان‌ها، و خوشه‌های کهکشانی) را توضیح می‌دهد.