سیستمهای ستارهی نوترونی دوتایی از مهمترین منابع امواج گرانشی قابل آشکارسازی توسط تداخلسنج پیشرفتهی لایگو۱ به شمار میروند. این سیستمها همچنین بهترین کاندید برای توضیح منشا انفجارهای پرتو گاما و دیگر تابشهای الکترومغناطیسی پرانرژی هستند. از اینرو مطالعهی شبیهسازیهای عددی این سیستمها در تعیین پارامترهای دوتایی نظیر جرم و معادلهی حالت ستارههای نوترونی در امواج گرانشی آشکارسازیشده امری اجتنابناپذیر است. نویسندگان این مقاله نشان دادهاند که با استفاده از مدل پدیدهشناختی حاصل از شبیهسازیهای عددی و با دردستداشتن اطلاعات رصدی امواج گرانشی بهدستآمده از حدود چند ده برخورد دوتایی ستارهی نوترونی در فاصلههای دورتر از ۱۰۰ مگاپارسک میتوان با تقریب خوبی شعاع ستارهی نوترونی را تخمین زد. این دقت عالی با تلفیق اندازهگیری جرم کل دوتایی قبل از برخورد و اندازهگیری پارامتر فشردگی (بهدستآمده از فرکانسهای نوسانی ابرستارهی نوترونی تشکیلشده بعد از برخورد) به دست میآید.
اطلاعات مربوط به معادلهی حالت ستارهی نوترونی از دو طریق به دست میآیند: فاز مارپیچی قبل از برخورد که ستارهها توسط نیروهای کشندی تغییر شکل میدهند، و فاز بعد از برخورد که ابرستارهی نوترونی ناپایدار تشکیل میشود. این نوسانات بسیار کوچک هستند و معمولا قابل اشکارسازی توسط لایگو نیستند، مگر اینکه سیستم دوتایی برخوردی خیلی نزدیک باشد و یا اینکه تعداد مشاهدات خیلی زیاد باشد. حتی با این وجود هم به تعداد زیادی مشاهده نیاز است که بتوان اطلاعات لازم را در حد معادلهی حالتهای حداکثری (خیلی سخت یا خیلی نرم) به دست آورد. روش دیگر استفاده از فرکانسهای مشخصهی سیگنال برخوردی و پسابرخوردی در امواج گرانشی است. به طورر کلی در هر برخورد سیستم ستارهی نوترونی دوتایی طیف امواج گرانشی پسابرخوردی دارای سه قلهی موج قوی یعنی فرکانس های f1,f2,f3 است که می توان از آنها جهت استخراج اطلاعات راجع به ساختار ستارههای نوترونی استفاده کرد.
نویسندگان این مقاله نشان دادهاند که چگونه میتوان از اطلاعات سیگنال موج گرانشی مرحلهی مارپیچی و پسابرخوردی حاصل از مشاهدهی تعداد کمی از دوتاییهای ستارهی نوترونی استفاده کرد و به تخمین بسیار خوبی از شعاع ستارهی نوترونی رسید. آنها با به کار گرفتن شبیهسازیهای ستارهی نوترونی موفق به ساخت یک مدل تحلیلی از امواج پسابرخوردی برای چهار معادلهی حالت مرجع شدهاند. این مدل به ما اجازه میدهد که خطای فرکانسهای f1 و f2 را (که میتوانند در مشاهدات لایگو بسیار بزرگ باشند) تخمین بزنیم. انها نشان دادهاند که این خطا برای تعداد حدود ۱۰۰ مشاهدهی سیستم دوتایی در فاصلههای ۱۰۰ تا ۳۰۰ مگاپارسکی برای معادلهی حالت سخت میتواند حدود ۲-۵ درصد و برای معادلهی حالت نرم حدود ۷-۱۲ درصد باشد. این مدل در تخمین دقت شعاع ستارهی نوترونی بسیار دقیقتر از مدلهای ارائه شدهی پیشین است.
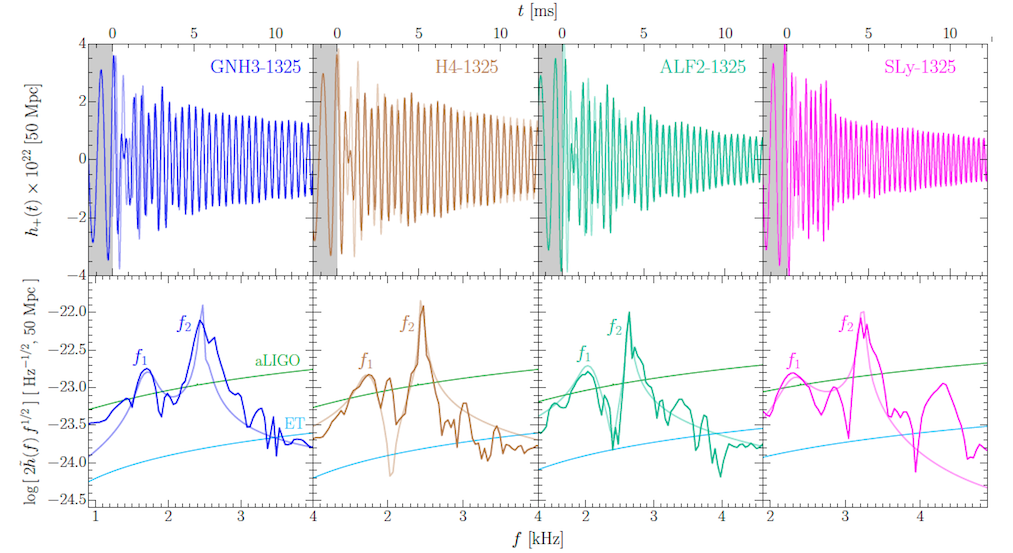
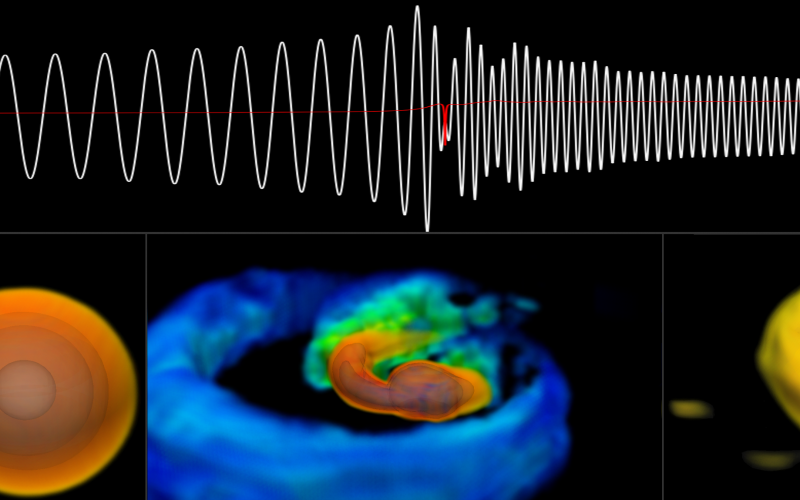
شکل ۱. پنل بالا: امواج گرانشی پسابرخوردی حاصل از شبیهسازی عددی دوتایی ستارهی نوترونی با جرم برابر ۱/۳۲۵ برابر جرم خورشید برای چهار معادله حالت مختلف (معادلهی حالت سخت به نرم از چپ به راست). موج حاصل از مدل تحلیلی ارائهشده در این مقاله با رنگ شفاف مشابه نشان داده شده است. پنل پایین: دامنههای طیفی متناظر با امواج گرانشی همراه با حساسیت فرکانس آشکارسازی توسط آشکارساز لایگو و تلسکوپ اینشتین.
امواج پسابرخوردی. شبیهسازیهای زوج ستارهی نوترونی نشان دادهاند که محتملترین جرم آسمانی که بعد از برخورد دو ستارهی نوترونی به وجود میآید، ابرستارههای نوترونی پرجرم و نسبتا پایداری هستند. این اجرام تا حدود چند ده میلیثانیه وجود دارند و بعد از آن فروپاشی میکنند و تبدیل به سیاهچاله میشوند. امواج گرانشی حاصل از این شبیهسازیها نشان میدهند که ارتباط تنگاتنگی بین نوسانات این امواج و درجهی سختی معادلهی حالت ستارهی نوترونی وجود دارد. بسته به جرم کل و نسبت جرمی سیستم دوتایی و معادلهی حالت ستارههای نوترونی برخوردکننده، امواج گرانشی پسابرخوردی میتوانند ویژگیهای طیفی برجستهای در سه فرکانس افزایشی f1, f2 و f3 داشته باشند. این قلهها در امواج گرانشی که یاداور خطوط طیفی در انتقالهای اتمی هستند، میتوانند اطلاعات جالبی دربارهی معادلهی حالت هستهای ستارهی نوترونی در بر داشته باشند. به طور کلی برجستهترین قله روی امواج گرانشی یعنی f2 بازتابدهندهی فرکانس اسپینی مود m=2 در ابرستارهی نوترونی تغییرشکل یافته است. ولی منشاء قلهی اول یعنی f1 هنوز ناشناخته باقی مانده است. با توجه با اینکه این قله بلافاصله بعد از برخورد شکل می گیرد و بعد از گذشت چند میلی ثانیه محو میشود، تصور عمومی بر این است که این فرکانس سیگنالی گذرا مربوط به برخورد هستههای ستارههای نوترونی است
مدلسازی دقیق از امواج دوتاییهای ستاره تونرونی مستلزم حل عددی معادلههای نسبیتی است. جهت بهینهکردن دقت و هزینهی محاسبات نسبیت عام عددی، نویسندگان این مقاله یک مدل پدیدهشناختی را برای ساختار موج پسابرخوردی معرفی کردهاند. این مدل با استفاده از برازش تحلیلی دامنهی زمانی بر روی کاتالوگ امواج حاصل از محاسبات عددی نسبیتی به دست آمده که در واقع میتوان آن را به صورت برهمنهی توابع سینوسی میرا با وابستگی زمانی تعریف کرد. برازش معرفیشده نه تنها سازگاری خوبی با طیف سیگنالها در نزدیکی فرکانس های f1 و f2 دارد بلکه همچنین تا حدود ۸۰ الی ۹۴ درصد مطابق با فاز سیگنال گرانشی است. بنابراین زمانی که این مدل با مدلهای تحلیلی نظیر محاسبات پسانیوتنی برای مرحلهی مارپیچی تلفیق میشود، مدل تحلیلی خوب و کاملی را برای سیگنال امواج گرانشی از کلیهی مراحل برخورد دوتایی ستاره نوترونی ارائه میدهند. پنل بالایی شکل ۱، دامنهی موج گرانشی با قطبش +h حاصل از حل عددی معادلات نسبیت و همچنین برازش مدل تحلیلی را بر روی چهار معادلهی حالت برای چشمهی امواج گرانشی (فاصلهی ۵۰ مگاپارسکی) نشان میدهد. پنل پایین در این شکل دامنهی طیفی متناظر (حاصلضرب فرکانس در تبدیل فوریه قطبش h+) و منحنی حساسیت اندازهگیری لایگو و تلسکوپ اینشتین را نشان میدهند.
دو ملاحظه در اینجا وجود دارد: اول اینکه چهار معادله حالت انتخابشده در این مقاله به نحو مناسبی گسترهی ممکن برای معادلات حالت سخت و نرم را فراهم میکند ولی همچنان با معادلات حالت خیلی نرم فاصله دارد. دوم اینکه این برازشها سیستمهای با جرم مساوی را به خوبی توصیف میکنند ولی همچنان میتوان آنها را با دقت خوبی برای سیستمهای دوتایی با جرم غیرمساوی (با نسبت جرمی بزرگتر از ۰/۸) نیز به کار برد. لازم به یادآوری است که آشکارسازی امواج پسابرخوردی حتی در دوتاییهای که در فاصله ۵۰ مگاپارسکی قرار دارند نیز بسیار دشوار است. به عنوان مثال برای یک برخورد دوتایی نسبت سیگنال به نویز برای آشکارساز لایگو حدود ۱/۸ است (هر چه این نسبت بزرگتر باشد سیگنال گرانشی أشکارسازیشده قویتر است). هرچند این نسبت کوچک باعث نمیشود که این امواج گرانشی اطلاعاتی نداشته باشند. جهت استخراج بهینهی این اطلاعات اگر تعداد قابل ملاحظهای مثلا ۱۰۰ دوتایی ستاره نوترونی را مشاهده کنیم، با کاهش خطا در اندازهگیری فرکانس f2 میتوانیم دقت در اندازهگیری پارامتر فشردگی ستارهی نوترونی را به حدود یک درصد برسانیم.
اندازهگیری شعاع ستاره نوترونی. به طور کلی با اندازهگیری فرکانسهای f1 و f2 و محاسبهی فشردگی از روی این فرکانسها (که نسبت جرم به شعاع ستاره نوترونی است) و با تخمین جرم ستارههای برخوردی از روی امواج گرانشی میتوان شعاع ستارهی نوترونی را تخمین زد. برای یک سیستم دوتایی که در فاصله ۳۰ مگاپارسکی قرار دارد، به علت قوی بودن امواج گرانشی، دقت اندازهگیری در فشردگی به کمتر از یک درصد میرسد. این بدین معنی است که خطای موجود در اندازهگیری شعاع ستارهی نوترونی به حدود ۱۲۵ متر خواهد رسید (شعاع ستارهی نوترونی در حد ۱۰-۱۲ کیلومتر است) که بسیار دقیقتر از تخمینهای مشابه دیگر است. در عالم واقعیت همهی ستارههای نوترونی دوتایی آنقدر به ما نزدیک نیستند که سیگنالی خیلی قوی داشته باشیم، پس برای دوتاییهای دورتر به ناچار سیگنال ضعیفتر و در نتیجه اندازهگیری فرکانسهای f1 و f2 بسیار مشکلتر میشود. در این صورت نیاز داریم تا مشاهدات بیشتری انجام دهیم تا اندازهگیری دقیقتری برروی فرکانس f2 داشته باشیم. جهت تخمینزدن فرکانس f2 برای جمعیت دوتاییهای مشاهدهشده در فواصل دورتر میتوان از شبیهسازیهای مونتکارلو استفاده کرد. دراین شبیهسازیها در هر آزمایش ۱۰۰ سیگنال امواج گرانشی ستارهی نوترونی دوتایی را که در ۱۰۰ سری زمانی نویز با تابع گاوسی تزریق شده، مورد استفاده قرار میگیرد و در نهایت مقدار میانگین فرکانس f2 به دست میآید. سپس با استفاده از رابطهی شبه جهانشمول ابتدا پارامتر فشردگی و بعد شعاع ستارهی نوترونی به دست میآید.
نتیجهگیری. در این مقاله روش جدیدی برای پیبردن به شعاع میانگین جمعیتی از ستارههای نوترونی موجود در دوتاییهای ستارهی نوترونی ارائه شده است که از هر دو فاز مارپیچی قبل از برخورد و بعد از برخورد استفاده میکند. این روش با دقت خوبی میتواند جایگزین روش تصحیحات کشندی شود که تنها از اطلاعات موجود در سیگنال مارپیچی استفاده میکند. به طور خاص مرحلهی پسابرخورد ما را قادر به اندازهگیری پارامتر فشردگی ستاره نوترونی میکند که به خوبی تکمیلکنندهی اندازهگیری مؤلفههای جرمی ستارههای برخوردکننده و در نهایت تخمین شعاع ستارهی نوترونی است. لازم به ذکر است که یافتههای این مقاله به دو دلیل محدودیت دارد: یکی به این دلیل که این مدل تنها محدود میشود به دوتاییها با جرم یکسان که البته با توجه به محاسبات به نظر میرسد که این مدل همچنان میتواند تخمین خوبی برای دوتاییهای با جرم متفاوت که نسبت سیگنال به نویز مشابهی دارند باشد. دوم اینکه با افزایش تعداد مشاهدات عدم قطعیت سیستماتیک ناشی از دقت محاسبات عددی بالا خواهد رفت که این با توجه به بالابودن هزینهی محاسبات عددی امری اجتنابناپذیر خواهد بود. در نهایت از آنجاییکه اثر معادلهی حالت در امواج گرانشی و همچنین خود سیگنال امواج گرانشی ممکن است بسیار ضعیف باشد، به کارگرفتن حداکثری اطلاعات سیگنالها جهت استخراج پارامترهای معادلهی حالت بسیار مهم است. تخمین پارامترهای معادلهی حالت میتواند به درک بهتر از مادهی هستهای موجود در ستارهی نوترونی و پیبردن به سازگاری مشخصههای امواج گرانشی در مراحل مختلف پیش از برخورد و پس از برخورد کمک کند.
(۱) LIGO
عنوان اصلی مقاله: Neutron-star Radius from a Population of Binary Neutron Star Mergers
نویسندگان: Sukanta Bose, et al
لینک مقالهی اصلی: https://arxiv.org/abs/1705.10850
گردآوری: فاطمه حسیننوری